近日，我院非线性统计物理团队关于交通流动力学模型的全局稳定性和非线性分岔分析论文被Nonlinear Dynamics接受发表。

该研究利用宏观变量与微观变量之间的转换关系，建立了同时考虑上坡和下坡的微观汽车跟随模型，得到了交通流的宏观连续性方程。讨论了宏观连续介质方程的摄动传播特性和稳定条件。对于初始平衡状态下的均匀流动，稳定性条件表明，在小扰动作用下，随着坡角的增大，上坡稳定性增大，下坡稳定性减小。此外，在大扰动条件下，采用波前展开技术对初始平衡状态下的均匀流动进行了全局稳定性分析。对于初始非均匀流动，在平衡点处进行Hopf分岔和鞍结点分岔等非线性分岔分析，交通流状态变化时存在亚临界Hopf分岔;因此，Hopf分岔所形成的极限环是不稳定的，得到了鞍结点分岔存在的条件。仿真结果验证了模型的稳定性条件，确定了临界密度范围。数值模拟结果表明，相空间中存在Hopf分岔，且鞍结点分岔的螺旋鞍点随坡角的变化而变化。同时，研究了上下坡夹角对密度波演化的影响。

交通流的宏观连续性方程：

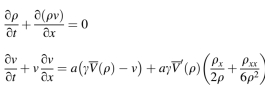
全局稳定条件：

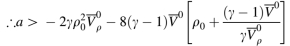
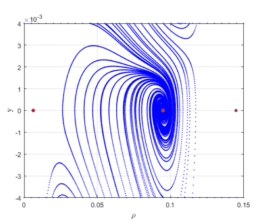
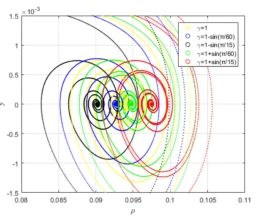
该工作获得国家自然科学基金、广西自然科学基金、广西研究生创新项目的资助。

论文作者：岑炳玲、薛郁、乔延峰、王艺、盘薇、何红第

论文链接：https://doi.org/10.1007/s11071-022-08032-y